Build Your Own Model¶
One important feature of orbit is to allow developers to build their own models in a relatively flexible manner to serve their own purpose. This tutorial will go over a demo on how to build up a simple Bayesian linear regression model using Pyro API in the backend with orbit interface.
Orbit Class Design¶
In version 1.1.0, the classes within Orbit are re-designed as such:
Forecaster
Model
Estimator
Forecaster¶
Forecaster provides general interface for users to perform fit and predict task. It is further inherited to provide different types of forecasting methodology:
[Stochastic Variational Inference (SVI)]
Full Bayesian
The discrepancy on these three methods mainly lie on the posteriors estimation where MAP will yield point posterior estimate and can be extracted through the method get_point_posterior(). Meanwhile, SVI and Full Bayesian allow posterior sample extraction through the method get_posteriors(). Alternatively, you can also approximate point estimate by passing through additional arg such as point_method='median' in the .fit() process.
To make use of a Forecaster, one must provide these two objects:
Model
Estimator
Theses two objects are prototyped as abstract and next subsections will cover how they work.
Model¶
Model is an object defined by a class inherited from BaseTemplate a.k.a Model Template in the diagram below. It mainly turns the logic of fit() and predict() concrete by supplying the fitter as a file (CmdStanPy) or a callable class (Pyro) and the internal predict() method. This object defines the overall inputs, model structure, parameters and likelihoods.
Estimator¶
Meanwhile, there are different APIs implement slightly different ways of sampling and optimization (for MAP). orbit is designed to support various APIs such as CmdStanPy and Pyro (hopefully PyMC3, Numpyro in the future!). The logic separating the call of different APIs with different interface is done by the Estimator class which is further inherited in PyroEstimator and StanEstimator.
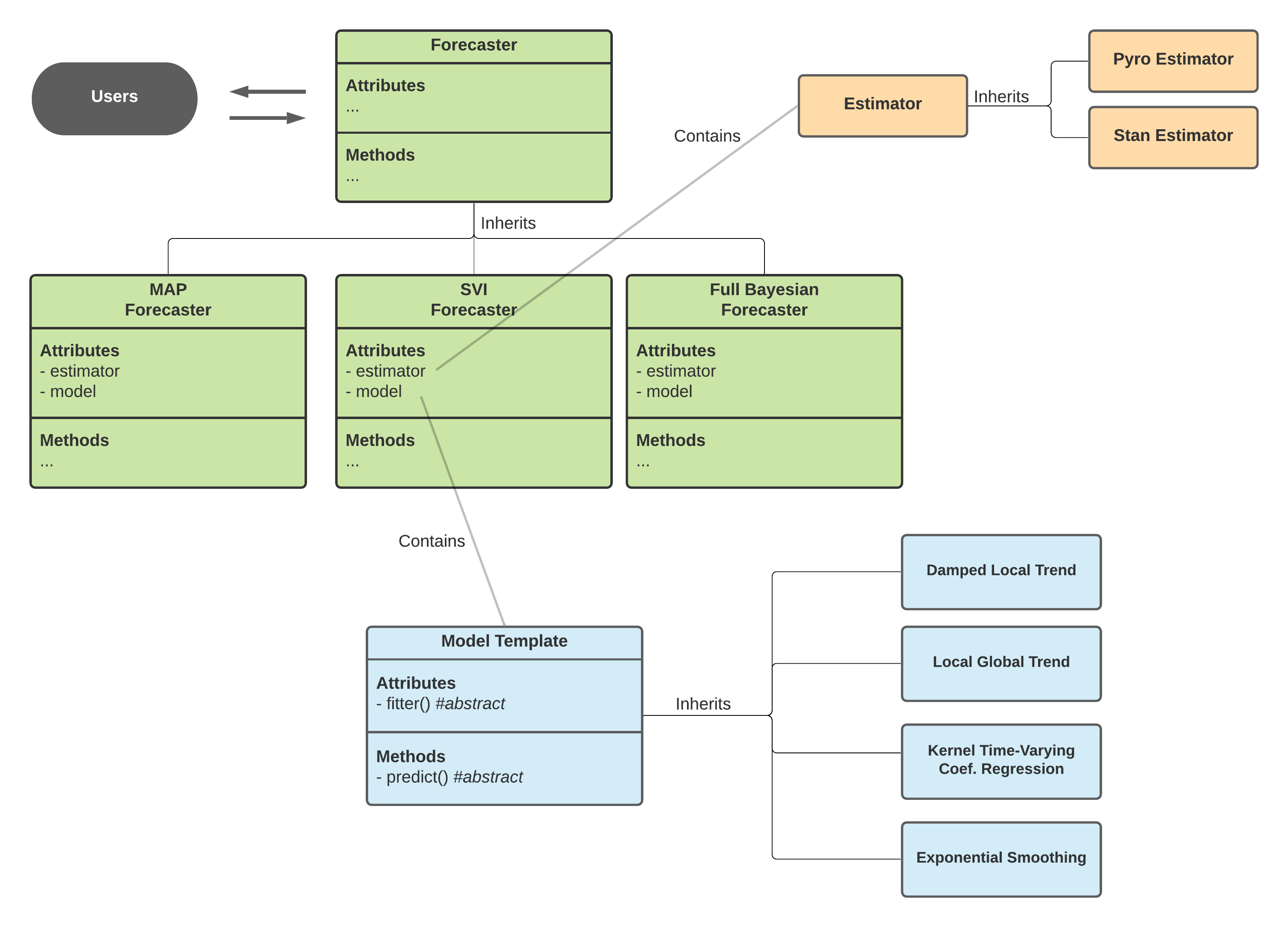
Diagram above shows the interaction across classes under the Orbit package design.
Creating a Bayesian Linear Regression Model¶
The plan here is to build a classical regression model with the formula below:
where \(\alpha\) is the intercept, \(\beta\) is the coefficients matrix and \(\epsilon\) is the random noise.
To start with let’s load the libraries.
[1]:
import pandas as pd
import numpy as np
import torch
import pyro
import pyro.distributions as dist
from copy import deepcopy
import matplotlib.pyplot as plt
import orbit
from orbit.template.model_template import ModelTemplate
from orbit.forecaster import SVIForecaster
from orbit.estimators.pyro_estimator import PyroEstimatorSVI
from orbit.utils.simulation import make_regression
from orbit.diagnostics.plot import plot_predicted_data
from orbit.utils.plot import get_orbit_style
plt.style.use(get_orbit_style())
%matplotlib inline
[2]:
print(orbit.__version__)
1.1.4.6
Since the Forecaster and Estimator are already built inside orbit, the rest of the ingredients to construct a new model will be a Model object that contains the follow:
a callable class as a fitter
a predict method
Define a Fitter¶
For Pyro users, you should find the code below familiar. All it does is to put a Bayesian linear regression (BLR) model code in a callable class. Details of BLR will not be covered here. Note that the parameters here need to be consistent .
[3]:
class MyFitter:
max_plate_nesting = 1 # max number of plates nested in model
def __init__(self, data):
for key, value in data.items():
key = key.lower()
if isinstance(value, (list, np.ndarray)):
value = torch.tensor(value, dtype=torch.float)
self.__dict__[key] = value
def __call__(self):
extra_out = {}
p = self.regressor.shape[1]
bias = pyro.sample("bias", dist.Normal(0, 1))
weight = pyro.sample("weight", dist.Normal(0, 1).expand([p]).to_event(1))
yhat = bias + weight @ self.regressor.transpose(-1, -2)
obs_sigma = pyro.sample("obs_sigma", dist.HalfCauchy(self.response_sd))
with pyro.plate("response_plate", self.num_of_obs):
pyro.sample("response", dist.Normal(yhat, obs_sigma), obs=self.response)
log_prob = dist.Normal(yhat[..., 1:], obs_sigma).log_prob(self.response[1:])
extra_out.update(
{"log_prob": log_prob}
)
return extra_out
Define the Model Class¶
This is the part requires the knowledge of orbit most. First we construct a class by plugging in the fitter callable. Users need to let the orbit estimators know the required input in addition to the defaults (e.g. response, response_sd etc.). In this case, it takes regressor as the matrix input from the data frame. That is why there are lines of code to provide this information in
_data_input_mapper- a list orEnumto let estimator keep tracking required data inputset_dynamic_attributes- the logic define the actual inputs i.e.regressorfrom the data frame. This is a reserved function being called inside Forecaster.
Finally, we code the logic in predict() to define how we utilize posteriors to perform in-sample / out-of-sample prediction. Note that the output needs to be a dictionary where it supports components decomposition.
[4]:
class BayesLinearRegression(ModelTemplate):
_fitter = MyFitter
_data_input_mapper = ['regressor']
_supported_estimator_types = [PyroEstimatorSVI]
def __init__(self, regressor_col, **kwargs):
super().__init__(**kwargs)
self.regressor_col = regressor_col
self.regressor = None
self._model_param_names = ['bias', 'weight', 'obs_sigma']
def set_dynamic_attributes(self, df, training_meta):
self.regressor = df[self.regressor_col].values
def predict(self, posterior_estimates, df, training_meta, prediction_meta, include_error=False, **kwargs):
model = deepcopy(posterior_estimates)
new_regressor = df[self.regressor_col].values.T
bias = np.expand_dims(model.get('bias'),-1)
obs_sigma = np.expand_dims(model.get('obs_sigma'), -1)
weight = model.get('weight')
pred_len = df.shape[0]
batch_size = weight.shape[0]
prediction = bias + np.matmul(weight, new_regressor) + \
np.random.normal(0, obs_sigma, size=(batch_size, pred_len))
return {'prediction': prediction}
Test the New Model with Forecaster¶
Once the model class is defined. User can initialize an object and build a forecaster for fit and predict purpose. Before doing that, the demo provides a simulated dataset here.
Data Simulation¶
[5]:
x, y, coefs = make_regression(120, [3.0, -1.0], bias=1.0, scale=1.0)
[6]:
df = pd.DataFrame(
np.concatenate([y.reshape(-1, 1), x], axis=1), columns=['y', 'x1', 'x2']
)
df['week'] = pd.date_range(start='2016-01-04', periods=len(y), freq='7D')
[7]:
df.head(5)
[7]:
| y | x1 | x2 | week | |
|---|---|---|---|---|
| 0 | 2.382337 | 0.345584 | 0.000000 | 2016-01-04 |
| 1 | 2.812929 | 0.330437 | -0.000000 | 2016-01-11 |
| 2 | 3.600130 | 0.905356 | 0.446375 | 2016-01-18 |
| 3 | -0.884275 | -0.000000 | 0.581118 | 2016-01-25 |
| 4 | 2.704941 | 0.364572 | 0.294132 | 2016-02-01 |
[8]:
test_size = 20
train_df = df[:-test_size]
test_df = df[-test_size:]
Create the Forecaster¶
As mentioned previously, model is the inner object to control the math. To use it for fit and predict purpose, we need a Forecaster. Since the model is written in Pyro, the pick here should be SVIForecaster.
[9]:
model = BayesLinearRegression(
regressor_col=['x1','x2'],
)
[10]:
blr = SVIForecaster(
model=model,
response_col='y',
date_col='week',
estimator_type=PyroEstimatorSVI,
verbose=True,
num_steps=501,
seed=2021,
)
[11]:
blr
[11]:
<orbit.forecaster.svi.SVIForecaster at 0x2a6164950>
Now, an object blr is instantiated as a SVIForecaster object and is ready for fit and predict.
[12]:
blr.fit(train_df)
2024-03-19 23:37:55 - orbit - INFO - Using SVI (Pyro) with steps: 501, samples: 100, learning rate: 0.1, learning_rate_total_decay: 1.0 and particles: 100.
2024-03-19 23:37:56 - orbit - INFO - step 0 loss = 27333, scale = 0.077497
INFO:orbit:step 0 loss = 27333, scale = 0.077497
2024-03-19 23:37:58 - orbit - INFO - step 100 loss = 12594, scale = 0.0092399
INFO:orbit:step 100 loss = 12594, scale = 0.0092399
2024-03-19 23:38:00 - orbit - INFO - step 200 loss = 12591, scale = 0.0095592
INFO:orbit:step 200 loss = 12591, scale = 0.0095592
2024-03-19 23:38:03 - orbit - INFO - step 300 loss = 12593, scale = 0.0094199
INFO:orbit:step 300 loss = 12593, scale = 0.0094199
2024-03-19 23:38:06 - orbit - INFO - step 400 loss = 12591, scale = 0.0092691
INFO:orbit:step 400 loss = 12591, scale = 0.0092691
2024-03-19 23:38:10 - orbit - INFO - step 500 loss = 12591, scale = 0.0095463
INFO:orbit:step 500 loss = 12591, scale = 0.0095463
[12]:
<orbit.forecaster.svi.SVIForecaster at 0x2a6164950>
Compare Coefficients with Truth¶
[13]:
estimated_weights = blr.get_posterior_samples()['weight']
The code below is to compare the median of coefficients posteriors which is labeled as weight with the truth.
[14]:
print("True Coef: {:.3f}, {:.3f}".format(coefs[0], coefs[1]) )
estimated_coef = np.median(estimated_weights, axis=0)
print("Estimated Coef: {:.3f}, {:.3f}".format(estimated_coef[0], estimated_coef[1]))
True Coef: 3.000, -1.000
Estimated Coef: 2.956, -0.976
Examine Forecast Accuracy¶
[15]:
predicted_df = blr.predict(df)
[16]:
_ = plot_predicted_data(train_df, predicted_df, 'week', 'y', test_actual_df=test_df, prediction_percentiles=[5, 95])
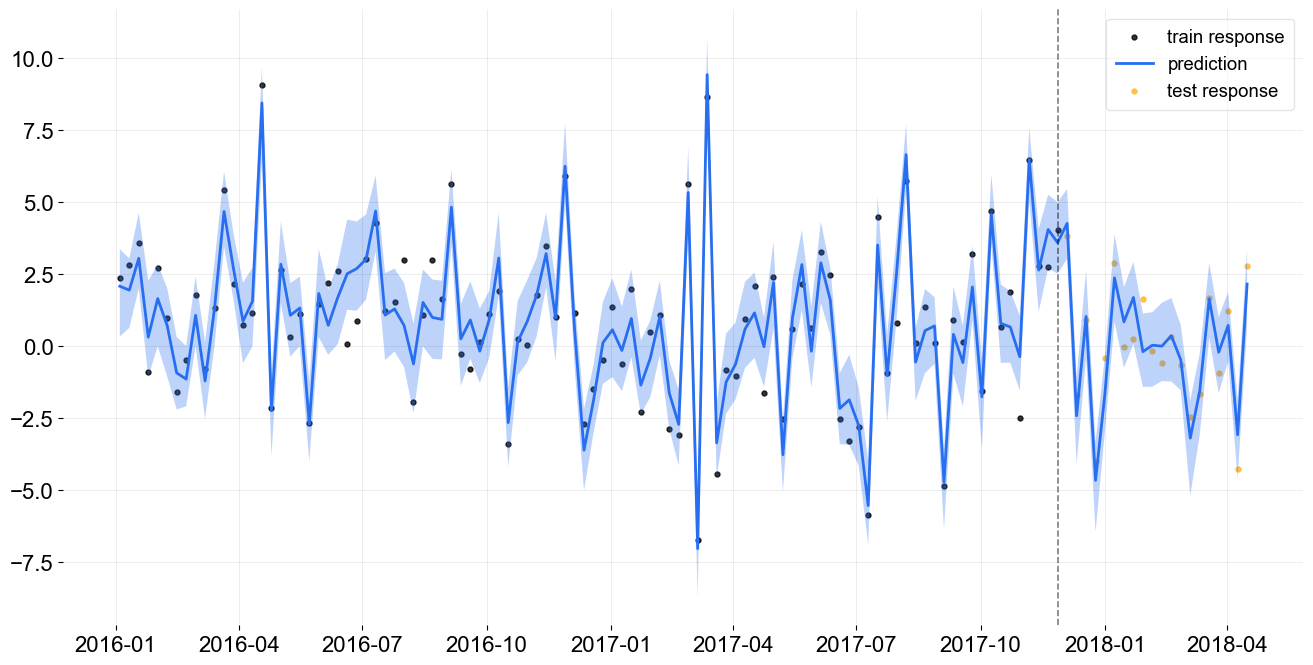
Additional Notes¶
In general, most of the diagnostic tools in orbit such as posteriors checking and plotting is applicable in the model created in this style. Also, users can provide point_method='median' in the fit() under the SVIForecaster to extract median of posteriors directly.