Local Global Trend (LGT)

In this section, we will cover:

• LGT model structure

• difference between DLT and LGT

• syntax to call LGT classes with different estimation methods

LGT stands for Local and Global Trend and is a refined model from Rlgt (Smyl et al., 2019). The main difference is that LGT is an additive form taking log-transformation response as the modeling response. This essentially converts the model into a multiplicative with some advantages (Ng and Wang et al., 2020). However, one drawback of this approach is that negative response values are not allowed due to the existence of the global trend term and because of that we start to deprecate the support of regression of this model.

%matplotlib inline

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

import orbit
from orbit.models import LGT
from orbit.diagnostics.plot import plot_predicted_data
from orbit.diagnostics.plot import plot_predicted_components
from orbit.utils.dataset import load_iclaims

print(orbit.__version__)

1.1.4.6

Model Structure

\[\begin{split}\begin{align*} y_{t} &= \mu_t + s_t + \epsilon_t \\ \mu_t &= l_{t-1} + \xi_1 b_{t-1} + \xi_2 l_{t-1}^{\lambda}\\ \epsilon_t &~\sim \mathtt{Student}(\nu, 0, \sigma)\\ \sigma &~\sim \mathtt{HalfCauchy}(0, \gamma_0) \end{align*}\end{split}\]

with the update process,

\[\begin{split}\begin{align*} l_t &= \rho_l(y_t - s_t) + (1-\rho_l)l_{t-1}\\ b_t &= \rho_b(l_t - l_{t-1}) + (1-\rho_b)b_{t-1}\\ s_{t+m} &= \rho_s(y_t - l_t ) + (1-\rho_s)s_t \end{align*}\end{split}\]

Unlike DLT model which has a deterministic trend, LGT introduces a hybrid trend where it consists of

• local trend takes on a fraction \(\xi_1\) rather than a damped factor

• global trend is with a auto-regrssive term \(\xi_2\) and a power term \(\lambda\)

We will continue to use the iclaims data with 52 weeks train-test split.

# load data
df = load_iclaims()
# define date and response column
date_col = 'week'
response_col = 'claims'
df.dtypes
test_size = 52
train_df = df[:-test_size]
test_df = df[-test_size:]

LGT Model

In orbit, we provide three methods for LGT model estimation and inferences, which are * MAP * MCMC (also providing the point estimate method, mean or median), which is also the default * SVI

Orbit follows a sklearn style model API. We can create an instance of the Orbit class and then call its fit and predict methods.

In this notebook, we will only cover MAP and MCMC methods. Refer to this notebook for the pyro estimation.

LGT - MAP

To use MAP, specify the estimator as stan-map.

lgt = LGT(
    response_col=response_col,
    date_col=date_col,
    estimator='stan-map',
    seasonality=52,
    seed=8888,
)

2024-03-19 23:39:41 - orbit - INFO - Optimizing (CmdStanPy) with algorithm: LBFGS.

%%time
lgt.fit(df=train_df)

CPU times: user 9.3 ms, sys: 16.8 ms, total: 26.1 ms
Wall time: 172 ms

<orbit.forecaster.map.MAPForecaster at 0x2919dccd0>

predicted_df = lgt.predict(df=test_df)

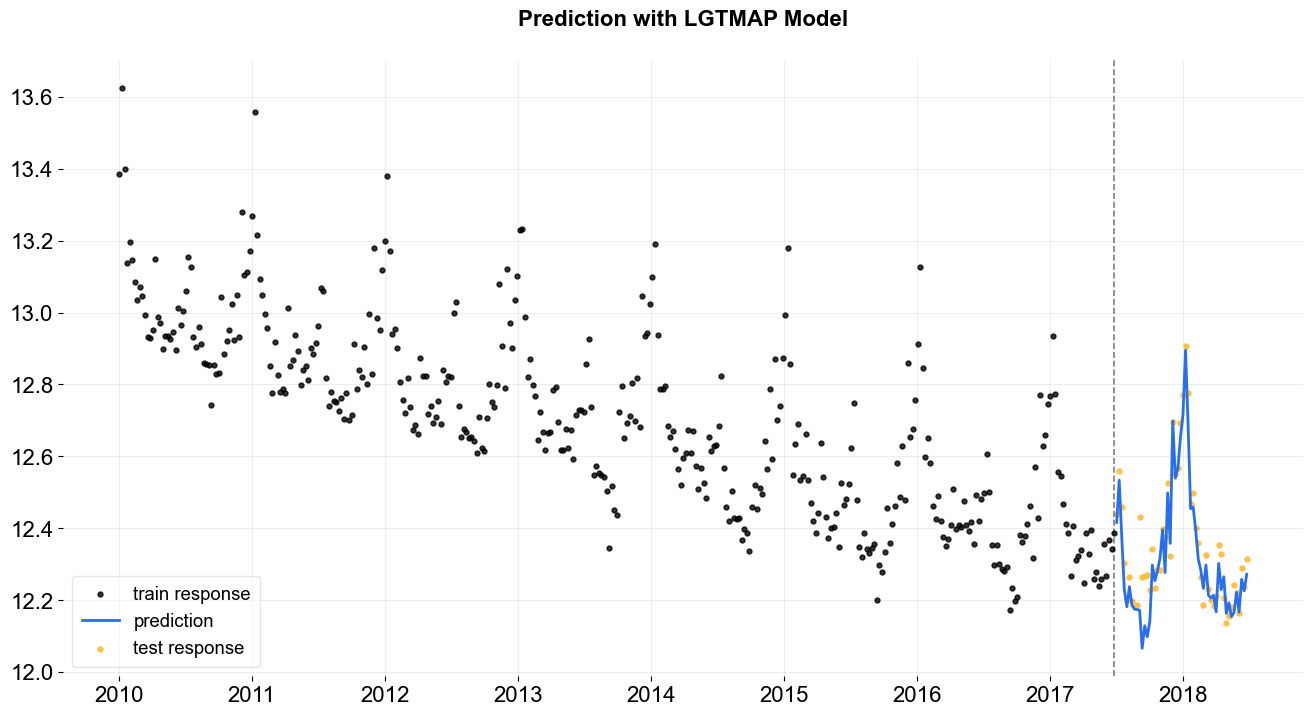
_ = plot_predicted_data(training_actual_df=train_df, predicted_df=predicted_df,
                        date_col=date_col, actual_col=response_col,
                        test_actual_df=test_df, title='Prediction with LGTMAP Model')

LGT - MCMC

To use MCMC sampling, specify the estimator as stan-mcmc (the default).

• By dedault, full Bayesian samples will be used for the predictions: for each set of parameter posterior samples, the prediction will be conducted once and the final predictions are aggregated over all the results. To be specific, the final predictions will be the median (aka 50th percentile) along with any additional percentiles provided. One can use .get_posterior_samples() to extract the samples for all sampling parameters.

• One can also specify point_method (either mean or median) via .fit to have the point estimate: the parameter posterior samples are aggregated first (mean or median) then conduct the prediction once.

LGT - full

lgt = LGT(
    response_col=response_col,
    date_col=date_col,
    seasonality=52,
    seed=2024,
    stan_mcmc_args={'show_progress': False},
)

%%time
lgt.fit(df=train_df)

2024-03-19 23:39:42 - orbit - INFO - Sampling (CmdStanPy) with chains: 4, cores: 8, temperature: 1.000, warmups (per chain): 225 and samples(per chain): 25.

CPU times: user 87.1 ms, sys: 36.9 ms, total: 124 ms
Wall time: 5.13 s

<orbit.forecaster.full_bayes.FullBayesianForecaster at 0x2a4bc4090>

predicted_df = lgt.predict(df=test_df)

predicted_df.tail(5)

	week	prediction_5	prediction	prediction_95
47	2018-05-27	12.114602	12.250131	12.382320
48	2018-06-03	12.058250	12.173431	12.272940
49	2018-06-10	12.164898	12.253941	12.387880
50	2018-06-17	12.138711	12.241891	12.362063
51	2018-06-24	12.182641	12.284261	12.397172

lgt.get_posterior_samples().keys()

dict_keys(['l', 'b', 'lev_sm', 'slp_sm', 'obs_sigma', 'nu', 'lgt_sum', 'gt_pow', 'lt_coef', 'gt_coef', 's', 'sea_sm', 'loglk'])

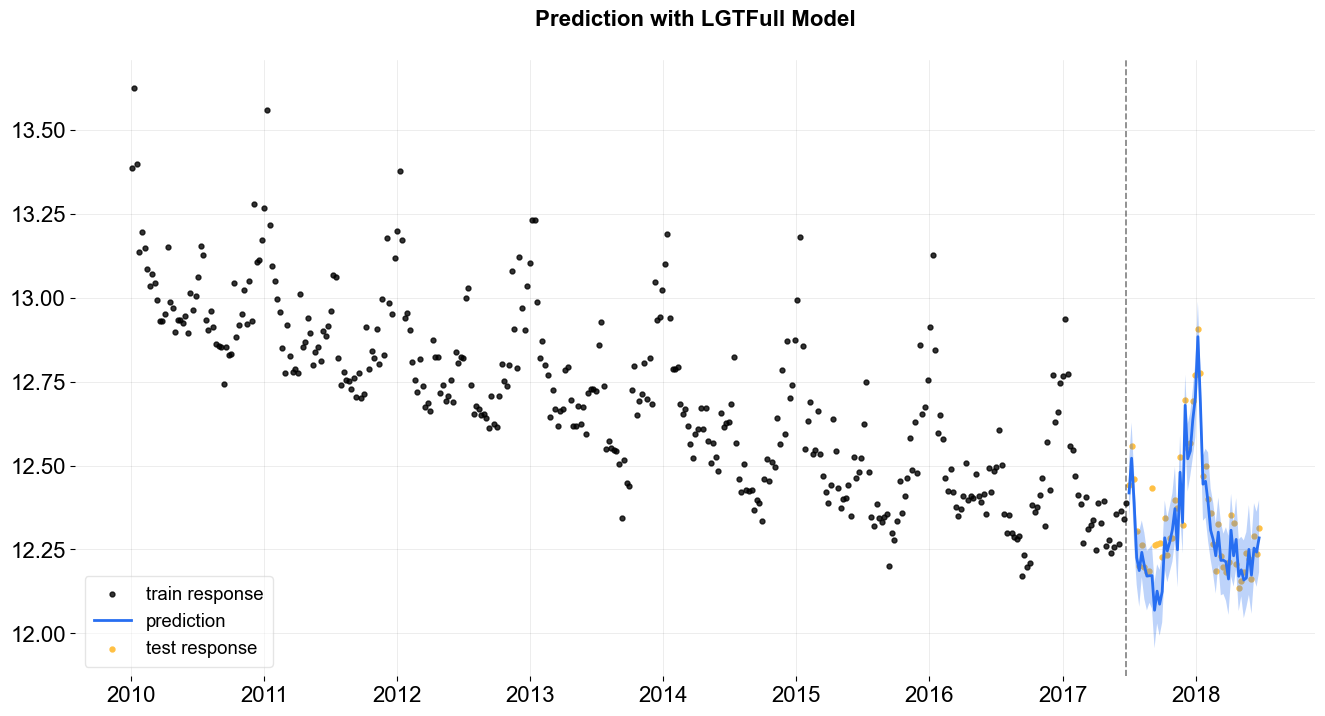
_ = plot_predicted_data(training_actual_df=train_df, predicted_df=predicted_df,
                    date_col=lgt.date_col, actual_col=lgt.response_col,
                    test_actual_df=test_df, title='Prediction with LGTFull Model')

LGT - point estimate

lgt = LGT(
    response_col=response_col,
    date_col=date_col,
    seasonality=52,
    seed=2024,
    stan_mcmc_args={'show_progress': False},
)

%%time
lgt.fit(df=train_df, point_method='mean')

2024-03-19 23:39:47 - orbit - INFO - Sampling (CmdStanPy) with chains: 4, cores: 8, temperature: 1.000, warmups (per chain): 225 and samples(per chain): 25.

CPU times: user 97.2 ms, sys: 41.7 ms, total: 139 ms
Wall time: 4.64 s

<orbit.forecaster.full_bayes.FullBayesianForecaster at 0x2a4d2add0>

predicted_df = lgt.predict(df=test_df)

predicted_df.tail(5)

	week	prediction
47	2018-05-27	12.210257
48	2018-06-03	12.145213
49	2018-06-10	12.239412
50	2018-06-17	12.207138
51	2018-06-24	12.253422

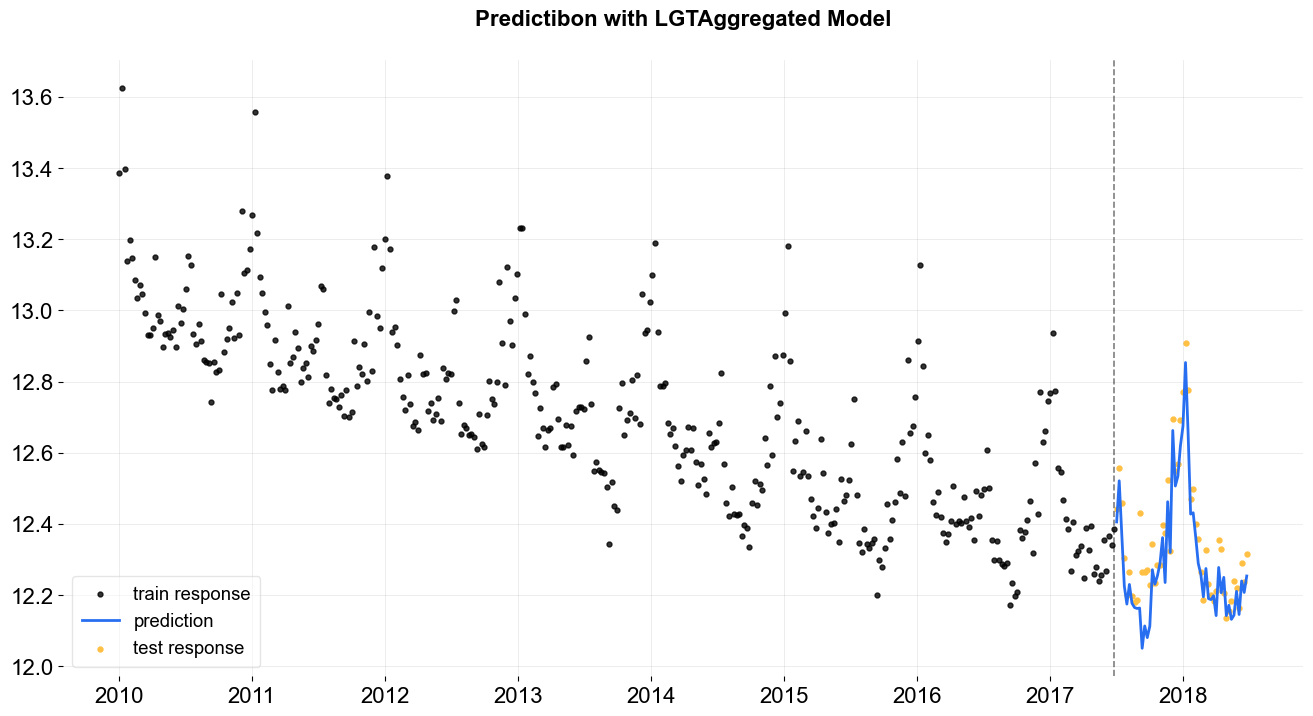
_ = plot_predicted_data(training_actual_df=train_df, predicted_df=predicted_df,
                    date_col=lgt.date_col, actual_col=lgt.response_col,
                    test_actual_df=test_df, title='Predictibon with LGTAggregated Model')