Quick Start¶
This session covers topics:
a forecast task on iclaims dataset
a simple Bayesian ETS Model using
CmdStanPyposterior distribution extraction
tools to visualize the forecast
Load Library¶
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import orbit
from orbit.utils.dataset import load_iclaims
from orbit.models import ETS
from orbit.diagnostics.plot import plot_predicted_data
[2]:
print(orbit.__version__)
1.1.4.6
Data¶
The iclaims data contains the weekly initial claims for US unemployment (obtained from Federal Reserve Bank of St. Louis) benefits against a few related Google trend queries (unemploy, filling and job) from Jan 2010 - June 2018. This aims to demo a similar dataset from the Bayesian Structural Time Series (BSTS) model (Scott and Varian 2014).
Note that the numbers are log-log transformed for fitting purpose and the discussion of using the regressors can be found in later chapters with the Damped Local Trend (DLT) model.
[3]:
# load data
df = load_iclaims()
date_col = 'week'
response_col = 'claims'
df.dtypes
[3]:
week datetime64[ns]
claims float64
trend.unemploy float64
trend.filling float64
trend.job float64
sp500 float64
vix float64
dtype: object
[4]:
df.head(5)
[4]:
| week | claims | trend.unemploy | trend.filling | trend.job | sp500 | vix | |
|---|---|---|---|---|---|---|---|
| 0 | 2010-01-03 | 13.386595 | 0.219882 | -0.318452 | 0.117500 | -0.417633 | 0.122654 |
| 1 | 2010-01-10 | 13.624218 | 0.219882 | -0.194838 | 0.168794 | -0.425480 | 0.110445 |
| 2 | 2010-01-17 | 13.398741 | 0.236143 | -0.292477 | 0.117500 | -0.465229 | 0.532339 |
| 3 | 2010-01-24 | 13.137549 | 0.203353 | -0.194838 | 0.106918 | -0.481751 | 0.428645 |
| 4 | 2010-01-31 | 13.196760 | 0.134360 | -0.242466 | 0.074483 | -0.488929 | 0.487404 |
Train-test split.
[5]:
test_size = 52
train_df = df[:-test_size]
test_df = df[-test_size:]
Forecasting Using Orbit¶
Orbit aims to provide an intuitive initialize-fit-predict interface for working with forecasting tasks. Under the hood, it utilizes probabilistic modeling API such as CmdStanPy and Pyro. We first illustrate a Bayesian implementation of Rob Hyndman’s ETS (which stands for Error, Trend, and Seasonality) Model (Hyndman et. al, 2008) using CmdStanPy.
[6]:
ets = ETS(
response_col=response_col,
date_col=date_col,
seasonality=52,
seed=2024,
estimator="stan-mcmc",
stan_mcmc_args={'show_progress': False},
)
[7]:
%%time
ets.fit(df=train_df)
2024-03-19 23:42:10 - orbit - INFO - Sampling (CmdStanPy) with chains: 4, cores: 8, temperature: 1.000, warmups (per chain): 225 and samples(per chain): 25.
CPU times: user 42.9 ms, sys: 24.3 ms, total: 67.2 ms
Wall time: 613 ms
[7]:
<orbit.forecaster.full_bayes.FullBayesianForecaster at 0x2a5274b50>
[8]:
predicted_df = ets.predict(df=test_df)
[9]:
_ = plot_predicted_data(train_df, predicted_df, date_col, response_col, title='Prediction with ETS')
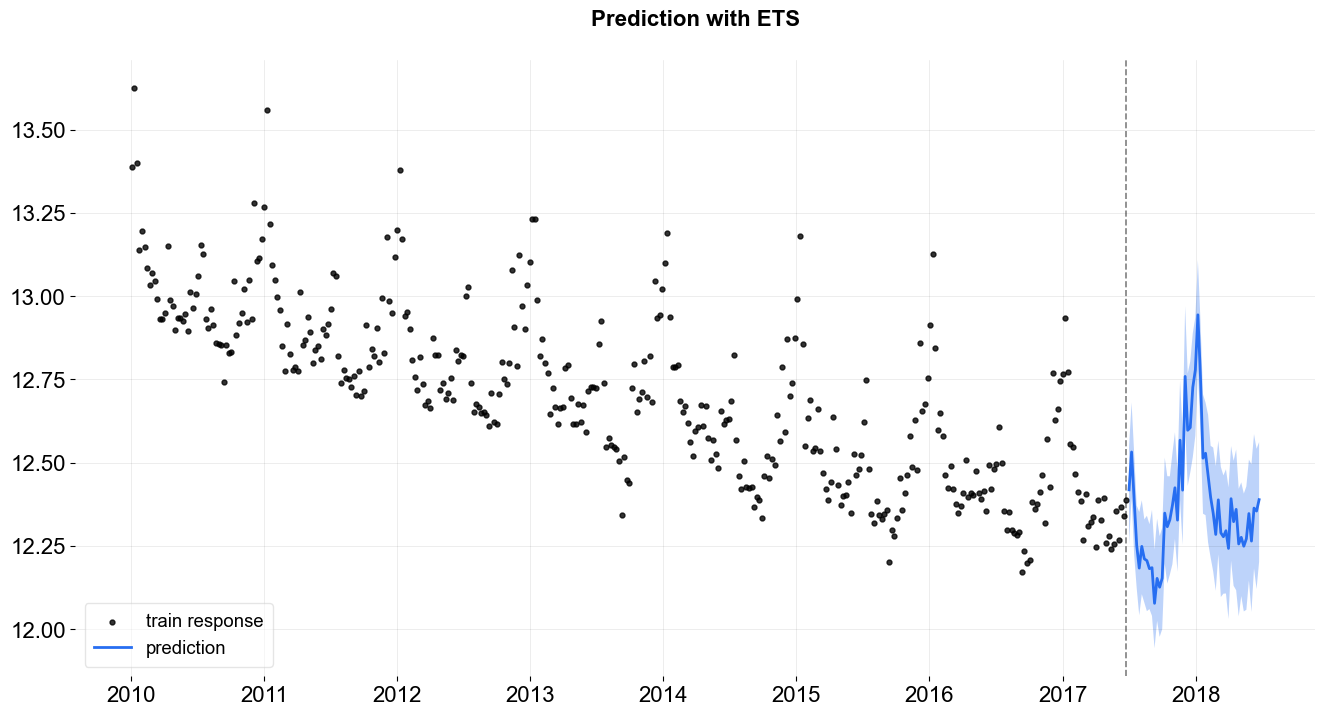
Extract and Analyze Posterior Samples¶
Users can use .get_posterior_samples() to extract posterior samples in an OrderedDict format.
[10]:
posterior_samples = ets.get_posterior_samples()
posterior_samples.keys()
[10]:
dict_keys(['l', 'lev_sm', 'obs_sigma', 's', 'sea_sm', 'loglk'])
The extracted parameters posteriors are pretty much compatible diagnostic with arviz. To do that, users can set permute=False to preserve chain information.
[11]:
import arviz as az
posterior_samples = ets.get_posterior_samples(permute=False)
# example from https://arviz-devs.github.io/arviz/index.html
az.style.use("arviz-darkgrid")
az.plot_pair(
posterior_samples,
var_names=["sea_sm", "lev_sm", "obs_sigma"],
kind="kde",
marginals=True,
textsize=15,
)
plt.show()
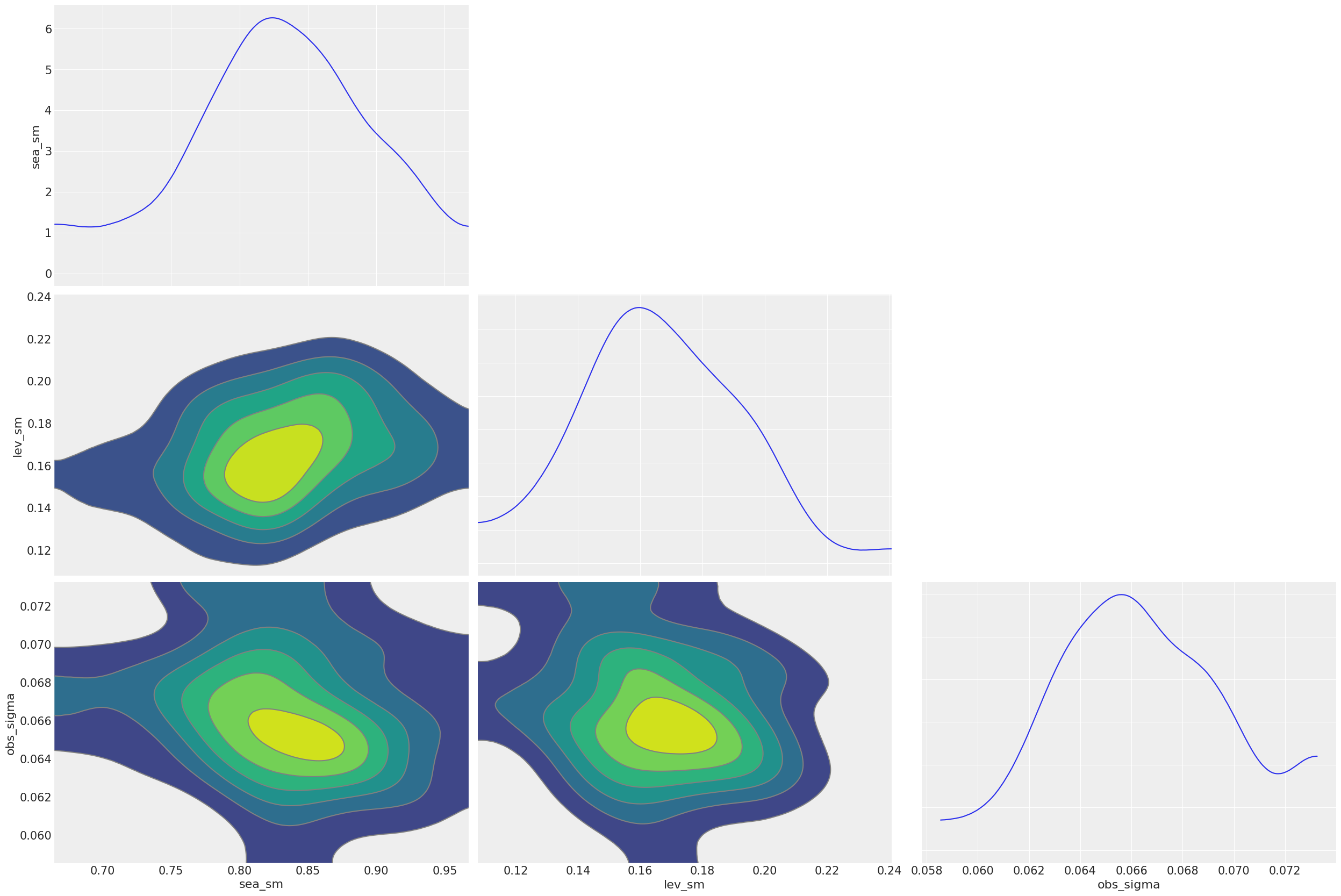
For more details in model diagnostics visualization, there is a subsequent section dedicated to it.